We will let P(i,j,e) stand for the state price of an elementary security (i is the time, j is the state, and e denotes that it is an elementary security). We note that P(0,0,e) = 1 since the "price," or value of $1 today is $1. Using this fact, we can work forward to compute the P(i,j) values at every node. The following are the equations we would use to move forward in the binomial lattice model:
The equation above would represent moving to the right once in our lattice.

The equation above would represent moving to the right and up diagonally once in our lattice.
The equation above would represent moving to the right once and up an integer between 0 and k+1 times in our lattice.
We then computed the forward prices for our short-rate lattice by using the forward equations and starting with the fact that P(0,0,e) = 1.
Our short-rate lattice:
and our elementary prices lattice corresponding to that:
Using these values, it becomes very easy to calculate derivative prices.
For example: say we want to calculate the price of a zcb at time 0 with maturity 4 and face value of 100. We simply add the elementary prices for time t=4 and multiply them by 100:
100 * (0.449 + .1868 + .2901 + .1992 + .0511) = 77.22 which is what we calculated before.
Another example:
A forward-start swap that begins at time t=1 and ends at time t=3. The notional principal is $1 million, the fixed swap rate is 7%, and the payments at time t=2 and t=3 are based on the fixed rate minus the floating rate that prevailed at times t=1 and t=2, respectively. (this swap is considered "forward-start" because it starts at time t=1 instead of t=0). The question: What is the value of the swap today, at time t=0?
To find the value, we do the following calculation:
Although this looks complicated, it is actually quite simple.
- The values (0.07 - xxx) are the payments received from this swap. The payments are the fixed rate minus the floating rate at times t=1 and t=2.
- The divisor underneath (0.07 - xxx) are the discounting factors. Remember than swap payments are made in arrears so although they payments are made for floating rates at time t=1 and t=2, the payments are made in time periods t=2 and t=3, so they must be discounted accordingly.
- The weights given to these cash flows are the corresponding elementary values on the elementary prices lattice.
The value of the forward-start swap at time t=0 ends up being $5800.




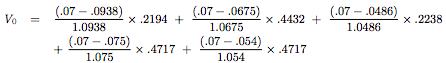
No comments:
Post a Comment