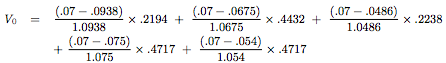Mortgage Pass-Throughs in Excel

In this lesson, we looked at mortgage pass-throughs in an excel spreadsheet.

I will not explain the walk through, but simply add the link to download the spreadsheet.

The spreadsheet can be found here:

https://d396qusza40orc.cloudfront.net/fe1/class_resources/MBS_Structure.xlsx

Prepayment Risk and Mortgage Pass-Throughs

In this lesson, we were introduced to prepayment risk and mortgage pass-throughs.  Prepayment risk refers to the ability of homeowners to prepay their mortgages (payments made in excess of the scheduled payment, B, is a prepayment).  This creates prepayment risk.  Mortgage pass-throughs are the simplest example of a MBS so we spent time learning about them.

Many homeowners prepay for multiple reasons;

• They must pay when they sell their home
• They can refinance at a lower interest rate
• They may default on their payments, so the insurer prepays the mortgage
• The home may be destroyed by flooding or fire, so the insurer pays the mortgage

Therefore, prepayment modeling is an important part of pricing MBSs.  

We then talked about the simplest type of MBS - the mortgage pass-through.  In practice, mortgages are usually sold on to third parties that can pool these mortgages together through securitization.  Such third parties are Ginnie Mae, Freddie Mac, or Fannie Mae, along with others.  MBSs that are issued by the three government agencies above are guaranteed against default, while MBSs that are issued by other third parties (non-agency mortgages) are not.  This alters the modeling of MBSs.  The simples type of MBS is the pass-through security where a group of mortgages is pooled together, then sold to investors, and investors receive monthly payments representing the interest and principal payments of the underlying mortgages.  The pass-through rate coupon, however, is strictly less than the average coupon rate of the underlying mortgages.  This is due to fees associated with servicing mortgages, as well as profit margins.  

WAC - Weighted Average Coupon Rate is a weighted average of the coupon rates in the mortgage pool with weights equal to mortgage amounts still outstanding

WAM - Weighted Average Maturity  is a weighted average of the remaining months to maturity of each mortgage in the mortgage pool with weights equal to the mortgage amounts outstanding.

They are prepayment conventions that are used by market participants when quoting yields and prices of MBSs. 

CPR - Conditional Prepayment Rate is the annual rate at which a given mortgage pool prepays.  It is expressed as percentage of the current outstanding principal level in the underlying mortgage pool

SMM - Single-Month Mortality Rate is the CPR converted to a monthly rate assuming monthly compounding.

These are related as follows:

In reality, the CPR is stochastic and depends on many economic variables.  However, market participants often use deterministic prepayment schedules as a mechanism to quote MBS yields and option-adjusted spreads.  

The standard benchmark for CPR is the Public Securities Association (PSA) benchmark.

The PSA benchmark assumes:

for 30 year mortgages.  In this case t is the number of months since the mortgage pool originated.  Slower and faster prepayment rates are then given as some percentage or multiple of the PSA benchmark.

Given a particular prepayment schedule, the average life of an MBS is defined as:

where P(k) is the principal (scheduled and projected) paid at time t, TP is the total principal, T is the total number of months, and we divide by 12 so that the average life is measured in years instead of months.  Average life decreases as PSA increases.

In practice, the price of an MBS is observed in the market place and a yield-to-maturity interest rate can be determined.  This rate is the rate that will make the present value of the expected cash flow equal to the market price.  The expected cash flows are determined based on some underlying prepayment assumptions such as 100 PSA, 200 PSA, 300 PSA, etc.  When the yield is quoted as an annual rate based on a semi-annual compounding, it is called a bond-equivalent yield.  These are very limited when evaluating an MBS and fixed income securities in general.  

An investor in a pass-through is exposed to interest rate risk in the fact that any fixed set of cash flows decreases as interest rates increase.  However, a pass-through investor is also exposed to prepayment risk, contraction risk and extension risk. 

When interest rates decline, prepayments tend to increase and the additional prepaid principal can only be invested at lower interest rates.  

When interest rated increase, prepayments tend to decreased and sot there is less prepaid principal that can be invested at higher rates. 

Introduction to Mortgage Mathematics and Mortgage Backed Securities

In this lesson we were introduced to basic mortgage mathematics and mortgage backed securities and the mortgage market.

The mortgage market accounted for 23.3% of the total outstanding amount of US bonds in Q3 2012.  These markets are huge and played a huge role in the financial crisis of 2008 and 2009.
MBSs are a particular class of asset-backed securities.  These are securities backed by underlying pools of securities, such as mortgages, credit card receivable,s auto loans, student loans, etc.  The process by which ABS are created is called "securitization."

Here is an image of how securitization works.  There are 10,000 mortgages and we combine them into one pool.  There are multiple tranches in the pool based on the risk characteristics of the loans.

There are many types of mortgages:

• level-payment mortgages
• adjustable-rate mortgages and
• balloon mortgages

to name a few.  We will only consider level-payment mortgages in these lessons.  A level payment mortgage is a mortgage in which the payment each month is constant over time.

We are going to consider a standard level-payment mortgage with the following assumptions:

• The initial mortgage price M(0) = M
• We assume equal periodic payments of $B
• The coupon rate  is c per period
• There are a total of n repayment periods
• After n payments, the mortgage principal and interest have all been paid (the mortgage is fully amortizing)

This means some of the payment, B, is principal, and some of the payment is interest.

If M(k) denotes the mortgage principal remaining after the k-th period, then

 


where M(n) = 0.
We can iterate this equation from M(0) = (1+c)*M(1)  - B all the way up to M(n-1) = (1+c)*M(n) - B to get the following equation:

but since M(n) = 0, we can plug k=n in this last equation we can say that:

So if we know M, n, and c, we can find the periodic payment amount for the mortg
age.
We can then substitute this B back into the equation above to get:

This tells us the value of the mortgage outstanding as a factor of the initial mortgage amount, the coupon rate, the number of total periods, and the current period.


Now suppose that we want to compute the present value of the mortgage in a deterministic world, with not possibilities of default or prepayments.
Assuming a risk-free interest rate of r per period, we can obtain the fair value of the mortgage as:

Here we are assuming that r is the borrowing interest rate for banks.  In practice, r will not be equal to c.  However,  if r=c, then F(0) = M(0).  In general r < c as banks must charge a higher interest rate so they can account for payment uncertainty, default, prepayment, servicing fees, and profits.

We can also decompose the monthly payment B into the interest component and the principal component.  The interest is:

is the interest that would be due in M(k)
The k-th payment is:

We can use this later to create principal-only and interest-only MBSs.

Pricing Credit Default Swaps

In this lesson, we continued the last lesson of pricing credit default swaps.

The value of the CDS to a buyer is going to be the risk-neutral value of the protection they receive when the bond defaults - the risk-neutral values of the premiums they pay.  We are going to assume that the default event is evenly distributed on the premium interval delta.

Now we will break apart these two factors that make up the value of the CDS.


The risk-neutral value of a single premium payment is: 

Remember that I(t(k)) shows that there is no default and B(t(k)) is the discounting factor (or the cash account or the value of a zcb).  Once again, as in the last lesson, we can break this down into simpler terms.

The risk-neutral value of of all the premium payments is just the sum of the above statement:

The risk-neutral value of the accrued interest if there is a default event between tau = (t(k-1), t(k)] is:

Since the default event is uniformly distributed on delta, the expected value of the uniform distribution of delta is simply (delta/2) which is how we get the above statement.

Therefore combining these values, the risk-neutral value of the premium and the accrued interest is:

We next moved on to the value of the protection.

The risk-neutral value of the protection is:

In this pricing, we assume that R is known, but in reality R is known only on default.  So we are assuming that these CDSs have been around for a while so we know what R will be.

The par spread, or S(par), is that makes the value of the spread that makes the contract equal to zero. S(par) is:

This is simply found by taking the value of the protection minus the value of the premium and accrued interest, setting this equal to zero, and solving for S. 

We then suppose that q(t(k)) = (1-h)*q(t(k) - 1).  We can then approximate the par spread to be:

Credit Default Swaps

In this lesson, we we introduced to credit default swaps.  We were introduced to how credit default swaps give us information about default probability and how these quantities can be used for hedging, investment, and speculation.

The seller of a credit default swap agrees to compensate the buyer in the event of a loan default or some other credit event on a reference entity in return for periodic premium payments.
The buyer pays period payments of d*S*N where:

• N is the notional principle amount of credit protection
• S is the coupon or the spread and
• d is a fraction of a year (d*S is the total coupon that has accumulated over the years)

this keeps on going until some credit event happens (usually a default).  At the next coupon date after this happens, the buyer has to pay the accrued interest d*S.  Also, the seller has to pay (1-R)*N where R is the recovery rate.  

Example:

Consider a 2-year CDS on a notional amount of $1 million with a spread S of 160 basis points (1.6%) and quarterly premium payments. 

Suppose a default occurs in month 16 of the 24 month protection plan and the recovery rate, R, is 45%.

The buyer:

The buyer pays fixed premiums in months 3,6,9,12,15 = (S*N)/4 = $4000

The accrued interest in month 18 (the next coupon date) is (S*N)/12 = $1333.33

The seller:

The default contingent protection payment in month 18 = (1-R)*N = $550,000

The basic model for CDS cash flows is as follows:

Let {t(k) = delta*k = 1,...,t(n)} denote the time of the coupon payments.  For quarterly payments delta = 1/4

If the reference entity is not in default at time t(k), the buyer pays the premium delta*S*N

If the reference entity defaults at time tau contained in (t(k-1), t(k)], then the contract terminates at time t(k).  The buyer pays the accrued interest (t(k) - tau)*S*N and the buyer receives (1-R)*N.  In the last example, the contract terminated at month 18 since default occurred at time tau=16 months between month 15 and month 18.

We then learned about CDS contract details.  CDS contract details were standardized by the International Swaps and Derivatives Association in 1999.  Changes were made in 2003, and 2009, and may happen again if CDS derivates lead to a financial global recession again.  There are so many different details in a contract because there are many difficult issues: how to determine if a credit event occurred, the recovery rate, the spread set for different bonds, when the coupon is paid (advance vs. arrears), and how the spread is quoted.  

The CDS spread S is approximates (1-R)*h where h is the hazard rate, or the conditional probability of default.  For fixed R, CDS spreads are directly proportional to the hazard rate h.  Thus CDS spreads, along with the recovery rate can help determine what the probability of default is for a given defaultable bond.

We then learned about the development and application history of CDS as well as their impact on the financial crisis and the sovereign debt crisis.  I have omitted this portion from this post. 

Pricing Defaultable Bonds

In this lesson, we extended the last lesson on pricing defaultable bonds to pricing coupon-bearing defaultable bonds as well as calibrating them.

We are assuming that the hazard rates, h(i,j) are state independent. This ensures that the default event is independent of the interest rate dynamics. We also let q(t) be the risk-neutral probability that the bond will survive until date t.  We then combine q(t) and h(i,j) into;

so as we can define the probability for survival in the next period based on survival up to that period.

Let I(t) denote the indicator variable that the bond survives up to time t;

The indicator variable that the default will occur at time t is I(t-1) - I(t).  It therefore follows that;
E[I(t)] = q(t).

Again, we assume that the random recovery rate, R, is independent of the interest rate dynamics as we did previously.  R denotes the fraction of the face value, F, paid on default.

We are going to assume the following information for the pricing process;

1. The current date is 0: t=0.
2. {t(1)...t(n)} are the futures dates at which the coupons are paid out
3. The coupon is paid on date t(k) only if I(t(k)) = 1.  Therefore the random cash flows associated with the coupon payment on dates t(k) is c*I(t(k))
4. The face value F is paid on date t(n) only if I(t(n)) = 1. Therefore the random cash flow associated with the face value payment on date t(n) is F*I(t(n)). 
5. The recovery R(t(k))*F is paid on date t(k) if the bond defaults on date t(k).  Therefore the random cash flow associated with the recovery on date t(k) is R(t(k))*F*[I(t(k-1)) - I(t(k))], where R is the recovery fraction, F is the face value, and the quantity [I(t(k-1)) - I(t(k))] denotes that the bond has defaulted.

Now that we have all these cash flows, we can price the bond by simply discounting all of the cash flows with respect to the correct risk-neutral probabilities. 

The price of the defaultable fixed coupon bond at time t=0 is given by:

The first term in the expectation, 

denotes the cash flow paid at time t(k) so they must be discounted at time t(k), which is what the B(t(k)) in the denominator represents (remember that B(t) is simply the value of the cash account at time t.

The second term in the expectation,

denotes the cash flow from the face value payment of the bond at time t(n), which is the B(t(n)) in the denominator.  B(t) is simply 1 since at time t=0, the value of the cash account is 1.

The third term in the expectation, 

is the random cash flow associated with the recovery if the bond defaults, discounted at time B(t(k)).  This quantity will equal 0 unless the bond defaults at time t(k).  

Since we assumed that the default is independent of interest rate dynamics, we can split the expectation up according to whether it is the expectation of default or the expectation of the interest rate dynamic.  In the following equation, each term in the equation above has been split into two expectations multiplied by each other.  The first expectation is the expectation of default and the second is the expectation of interest rate dynamics;

We can then substitute q for the expectation of default and we can substitute Z(0,t(k)) (zcb price) for the expectation of the short rate:

We can further simplify this equation by simply substituting out the zcb prices (Z(0,t(k)) for the discount rate up to time t(k):

Next we are going to calibrate the hazard rates.  First, we assume that the interest rate is deterministic and known (and even if it was not, we are able to calibrate it, as we did in previous lessons).  

We then denote the model price of the defaultable bonds as P(h) as a function of h = {h(0)...h(n-1)}.

We then denote the market price for the defaultable bonds as P(market).

For model calibration, take the model prices and the market prices, get the pricing error between them:

and minimize it:

We then did this numerically in an excel spreadsheet.  

Modeling Defaultable Bonds

In this lesson, we looked at defaultable bonds and how to model them.  In a later lesson, we will look at pricing them.

A defaultable bond is characterized by a coupon rate, c, a face value, F, and a recovery value, R, which is a random fraction of the value value recovered when the bond defaults.  We will model the term-structure of default using a 1-step default probability:



and we will calibrate h(t) to market prices. h(t) is the conditional probability that the bond will default over the period t to t+1, given the information available at time t: (F(t)).


When we previously modeled the binomial lattice, we had two parameters for each node: i and j.  The i parameter indicated the date: i=0...n and the j parameter indicated the state j=0...i for each time parameter.  For defaultable bonds we will "split" each node (i,j) by introducing a variable that encodes whether or not default has occurred before time i.  For example:

• (i,j,0) <- state j at time i with default time tau > i
• (i,j,1) <- state j at time i with default time tau ≤ i

Now we need to define the new risk-neutral transition probabilities for the binomial lattice.  

Here is one example of the possible transitions for one lattice:

and here are the transitions from no-default state (i,j,0):

and here are the transitions from default state (i,j,1):

Notice that there are much fewer transitions because a bond that has already defaulted cannot be un-defaulted.


We started modeling these bonds with the most simple example:
a default-free zero-coupon bond with expiration date T.  This bond pays $1 in every state at the expiration date T, and no default is possible.
The price of such a bond is Z(i,j,eta,T) where i is the date, j is the state, eta is the default state, and T is the expiration date.  Since default events do not effect default-free bonds: Z(i,j,1,T) = Z(i,j,0,T) = Z(i,j,T) with no default state.
By risk-neutral pricing:

which is exactly what we had previously.

We can calibrate the short-rate lattice using the market prices of default-free zcbs and other default-free instruments.


We then moved on to zero coupon bonds that are defaultable, but have no recovery.  These bonds pay $1 in every state at expiration T, provided that default has not occurred at any date t ≤T.  If default occurs at t≤T, then the bond pays $0.
By risk-neutral pricing:

which means that:

and approximately:

In this case E[i,Qbar] is the expectation of risk-neutral default-free probability.
The price of a zcb is set by discounting the expected value by (r(i,j) + h(i,j)), where h(i,j) is the 1-period credit spread.  The conditional probability of default h(i,j) is also called the hazard rate.  This is the probability of default given that no default has occurred up to time i.


We then moved on to zero coupon bonds that are defaultable and have recovery.  We assumed that the recovery R is random and independent of the default and the interest dynamics.
By risk-neutral pricing:

This makes sense, because here we will recover R instead of zero (like we did one example above).

In the next lesson we will talk about general bonds and how to use these general bonds to estimate the hazard rate.

Fixed Income Derivatives Pricing In Practice

In this lesson, we wrapped up our discussion of model calibration.

The pricing philosophy is the same for all types of models:

1. Specify a model under the Q(theta) dynamics where theta is a vector of parameters, such as a(i) and b(i).
2. Price all securities using the formula:

      3. Choose theta parameters such that the market prices of the liquid securities agree with the model             prices.

These three steps are formally known as the calibration procedure.

The calibration problem usually requires minimizing a sum of squares equation:

where:

P(i)(model) is the model price of the i-th calibration security

P(i)(market) is the model price of the i-th calibration security

w(i) is a positive weight reflecting the importance of the i-th security or the confidence we have in its market price

theta(prev) = previously calibrated model parameters

and lambda is a parameter reflecting relative importance of remaining close to the previous calibration.

Once we have minimized this equation we can use the model to hedge or price more illiquid securities.

One problem, however, is that this equation is very difficult to solve.  It is a non-convex optimization problem with many local minima and therefore many solutions.  As market conditions change from minute-to-minute and hour-to-hour, we may need to recalibrate the model frequently.  If the model was in fact, "right," then we would only need to calibrate once.  So in practice our model is not right, and markets are too complex for there to be a "right model." However, through risk-neutral pricing at the model level, we can extrapolate/interpolate in an arbitrage free manner.  

Pricing A Payer Swaption in a BDT Model

In this lesson, we used the BDT model to price a payer swaption.

We are pricing a 2-8 payer swaption.  The 2 and 8 mean that the option is an option to enter an 8 year swap in 2 years time, and since swaps have payments made in arrears, the payments would be made in years 3-10.  The "payer" part of the swaption simply means that if the option is exercised, the exerciser pays the fixed rate and receives the floating rate.  This option would have been extremely profitable if bought at the bottom of the recession, when interest rates were near 0%.   This means we will be using a 10-period lattice.

We will also assume that b(i) = b = 0.005 for all i.  Remember that b(i) is the volatility of the short-rate.  By assuming b=0.005 for all i, we are assuming a constant volatility.  We will change this assumption later.

We are going to assume a notional principal of $1 million.  Let S(2) denote the value of the swap at time t=2.  We can compute this price by starting at the value of the swap at time t=10 and discounting backward from t=10 to t=2.  Once we have the values at time t=2, we determine whether the option will be exercised at t=2 by the value of the swaption: max(0,S(2)).  We then discount these values back to find the swaption price at t=0.

Assuming that we have calibrated the zcb according to the steps above with a b =0.005, we find that the swaption price is $13,339.  If we then doubled b to b=0.010, we find a swaption price of $19,497.  This is about 50% higher than our original price.  This is a very significant difference in the swaption prices.  Swaption prices clearly depend on the volatility of the market.  This is apparent because increasing volatility means that there is increasing upside that the short rate will be higher, and therefore the swaption will be worth more.  However, with increasing volatility there is not increasing downside since the swaption is worth the max(0,S(2)) so if the short-rate is negative then the swaption will simply not be exercised.

Here we can see how important it is to calibrate the BDT model according to different observations of volatility.  We want the calibration to be "close" to the securities we want to price with the calibrated model.  For example a zcb does not depend much on volatility, while caplets and floorlets are much more dependent on the volatility in the model.  More of this will be discussed in later lessons.

Model Calibration

In this lesson, we are taking the previously developed binomial lattice model and calibrating it so that the prices in the model agree with the corresponding market prices.  There are too many free parameters in the model, so we fix some parameters: q = 1-q = 0.50. and some some parametric form for for r(i,j) short-terms.  We will focus on the Black-Derman-Toy (BDT) Model.

The BDT model assumes that the interest rate at node N(i,j) is given by r(i,j) = a(i)*e^(b(i)*j) or in log terms: log(r(i,j)) = log(a(i)) + b(i)*j where log(ai) is a drift parameter for log(r) and b(i) is a volatility parameter for log(r).  Now we need to calibrate the model to the observed term-structure in the market.  This is done by choosing different a(i)'s and b(i)'s to match market models.  We can do this by using the Solver add-in in MS Excel, but we can also do this in Matlab or R.

To start an example, let us assume that we have an n-period binomial lattice, as usual.  We will let s(1)...s(n) be the term-structure of interest rates observed in the market.  We will also assume (for now) that b(i) = b for all i.  This is a very strong assumption and we will change it in the future.

We know that:

since this is just the definition of elementary prices of a zcb.
We can replace the right hand side of this equation with the forward equations from the last lesson:

where the first term is equal to P(i,0,e), the second term is equal to P(i,j,e) when j is between 1 and (i-1) and the third term is equal to P(i,i,e).  We can then begin solving for all the a(i)'s.  We could simply plug in i=1 then i=2 all the way up to i=n.  After simplifying and solving, we would have the formula for a(i) and we would be able to get the spot rate from the formula above: log(r(i,j)) = log(a(i)) + b(i)*j.  We can also use MS Excel Solver add-in to do this for us.  We then did exactly that in this module but I have omitted it from this blog post as an exercise for the reader.

The Forward Equations

In this lesson, we learned about forward equations.  Forward equations allow us to price elementary securities.  Elementary securities are securities that pay $1 at a specific time i and a specific state j, and pay $0 at every other time and state combination.  By using forward equations, we will be able to price elementary securities very easily.

We will let P(i,j,e) stand for the state price of an elementary security (i is the time, j is the state, and e denotes that it is an elementary security).  We note that P(0,0,e) = 1 since the "price," or value of $1 today is $1.  Using this fact, we can work forward to compute the P(i,j) values at every node.   The following are the equations we would use to move forward in the binomial lattice model:

The equation above would represent moving to the right once in our lattice.







The equation above would represent moving to the right and up diagonally once in our lattice.

The equation above would represent moving to the right once and up an integer between 0 and k+1 times in our lattice.


We then computed the forward prices for our short-rate lattice by using the forward equations and starting with the fact that P(0,0,e) = 1.

Our short-rate lattice:

and our elementary prices lattice corresponding to that:

Using these values, it becomes very easy to calculate derivative prices.
For example: say we want to calculate the price of a zcb at time 0 with maturity 4 and face value of 100.  We simply add the elementary prices for time t=4 and multiply them by 100:
100 * (0.449 + .1868 + .2901 + .1992 + .0511) = 77.22 which is what we calculated before.


Another example:
A forward-start swap that begins at time t=1 and ends at time t=3.  The notional principal is $1 million, the fixed swap rate is 7%, and the payments at time t=2 and t=3 are based on the fixed rate minus the floating rate that prevailed at times t=1 and t=2, respectively.  (this swap is considered "forward-start" because it starts at time t=1 instead of t=0).  The question:  What is the value of the swap today, at time t=0?


To find the value, we do the following calculation:

Although this looks complicated, it is actually quite simple.

• The values (0.07 - xxx) are the payments received from this swap.  The payments are the fixed rate minus the floating rate at times t=1 and t=2.
• The divisor underneath (0.07 - xxx) are the discounting factors.  Remember than swap payments are made in arrears so although they payments are made for floating rates at time t=1 and t=2, the payments are made in time periods t=2 and t=3, so they must be discounted accordingly.  
• The weights given to these cash flows are the corresponding elementary values on the elementary prices lattice. 

The value of the forward-start swap at time t=0 ends up being $5800.  

Fixed Income Derivatives: Swaps and Swaptions

In this lesson, we learned about pricing swaps and swaptions.  We learned about swaps a few weeks ago.  A swaption is simply an option on a swap contract.

We want to price a swap based on our short-rate, r, lattice.  Once again, here is our lattice:

We want to price an interest rate swap with a fixed strike rate of 5% that expires at time t=6.  The first payment will be made at time t=1 and the final payment will be made at time t=6.  The payment will be (r(i,j) - K) if you are long, and will be -(r(i,j) - K) if you are short.  It will be made in arrears, so this payment will be made at time t=i+1.



To price the swap, we will want to, once again, start from the ending (time t=6), then work backwards.  However, since the payment at time t=6 is based on the short-rate at time t=5, we will simply start at the values for t=5 (discount by 1 period) and work backwards.  The formula for pricing the swap prices at times t=5 is as follows:

(r(5,j) - K) at time t=6 is worth (r(5,j)-K)/(1+r(5,j)) at time t=5 where 1/(1+r(5,j)) is the discounting factor for the difference between periods 5 and 6.

The next step in pricing the swap will be working backwards in the lattice.  In this regard it will differ from what we have done previously since a swap will contain intermediate coupon payments.  So we must use the formula we previously had for risk-neutral pricing with intermediate coupon payments.  This formula is:
S(t) = E[(S(t+1) + C(t+1))/(1+r(t))]
where C(t+1) is simply (r(t,j) - K) at the node in which it is being calculated. An example is provided below the lattice:

And here is the example for node N(2,2):

We then moved on to pricing swaptions.  A swaption is simply an option on a swap.  We priced a swaption on the swap we just developed.  We are going to assume that the option strike is 0% (this is not to be confused with the strike of 5%, or fixed rate, on the underlying swap) and the swaption expiration is at t=3.
Therefore at time t=3, the owner of the swaption has the right to exercise and have ownership of the underlying swap for a strike value of 0.  So the payoff of the swaption is: max(0,S(3)) where S(3) is the underlying swap price.

In order to price this swaption, we will take max(0,S(3)) for time t=3 of the underlying swap, then simply work backwards in our lattice using risk-neutral pricing.  However, we will not be factoring in the intermediate cash flows for this lattice since the holder of the swaption will not get the cash flows until the exercise at time t=3.  Below is the swaption lattice with the values of the swaption replacing the values of the swap in blue: