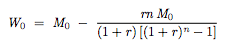Risks of Principal-Only and Interest-Only MBS

In this lesson, we looked at the risks and exposures of interest-only mortgage backed securities and principal-only mortgage backed securities.

We are going to measure risk by duration.  The duration of a cash flow is a weighted average of the times at which each component of the cash flow is received.  The principal stream has a longer duration than the interest stream of a mortgage since as the age of the mortgage increases, the interest payments will decrease (since they depend on the amount of the mortgage that is yet unpaid) and the principal payments will become a larger part of each monthly payment.  

If we let D(p) denote the duration of the principal stream then:

Where we divide by 12 to convert duration in annual units, rather than monthly units.  We can rewrite this as:

D(p) = the sum from k=1 to n of w(k)*k where 

w(k) = 1/(12*V(0)) * P(k)/(1+r)^k.

In this case is the weight given to each component.

Similarly, we can compute the duration of the interest stream as D(i):

Now we introduce the idea of prepayments.

The interest payment in period k is the same as before:

However, we must reassess the value of M(k) with each prepayment:

where ScheduledPrincipalPayment(k) is now P(k) = B - I(k) for period k.

The risk profiles of interest-only and principal-only MBSs are very different.

Principal-only MBS holders would like prepayments to increase, since they would like their payments earlier (due to the time value of money). 

Interest-only MBS holders would like prepayments to decrease, since the slower the mortgage is paid, the more interest will accrue on the mortgage.  

In an extreme case where all the mortgage holders of a particular MBS prepay their mortgages immediately after taking them out, the interest-only MBS holder will receive zero, since no interest will have been able to accrue on those mortgages.

Principal-Only and Interest-Only MBS

In this module, we discussed principal-only and interest-only mortgage backed securities.

As we discussed last lesson, the following equations correspond to the interest payments of a pass-through security and the principal payments:

remember that c is the coupon rate.  This is a level-payment mortgage.
Remember from last lesson that M(k) is:

and we can plug this into the expression for P(k) to give us:

The present value of these principal payments, V(0) is simply the sum of P(k) from k=1 to n over (1+r)^k (this is the discounting factor).  We can simplify this to:

This is the present value of the principal payments.  We can then use our expression for B from last lesson:

and substitute it into the present value equation to get:






We can also compute the present value of the interest payment revenue stream.  The present value, W(0) is simply the sum of I(k) from k=1 to n over (1+r)^k (this is the discounting factor):

This is very simple but it is much easier to recognize that the present value of the interest payments is equal to the total value of the mortgage, F(0), from last lesson, less the principal only payments.  F(0) is the fair value of the all the payments in the mortgage and is equal to:

As I said earlier, W(0) = F(0) - V(0), so:

and we can see that when r converges to c, this equal reduces to:

In the next lesson, we will look at the risks for each of these mortgage backed securities.

Mortgage Pass-Throughs in Excel

In this lesson, we looked at mortgage pass-throughs in an excel spreadsheet.

I will not explain the walk through, but simply add the link to download the spreadsheet.

The spreadsheet can be found here:

https://d396qusza40orc.cloudfront.net/fe1/class_resources/MBS_Structure.xlsx

Prepayment Risk and Mortgage Pass-Throughs

In this lesson, we were introduced to prepayment risk and mortgage pass-throughs.  Prepayment risk refers to the ability of homeowners to prepay their mortgages (payments made in excess of the scheduled payment, B, is a prepayment).  This creates prepayment risk.  Mortgage pass-throughs are the simplest example of a MBS so we spent time learning about them.

Many homeowners prepay for multiple reasons;

• They must pay when they sell their home
• They can refinance at a lower interest rate
• They may default on their payments, so the insurer prepays the mortgage
• The home may be destroyed by flooding or fire, so the insurer pays the mortgage

Therefore, prepayment modeling is an important part of pricing MBSs.  

We then talked about the simplest type of MBS - the mortgage pass-through.  In practice, mortgages are usually sold on to third parties that can pool these mortgages together through securitization.  Such third parties are Ginnie Mae, Freddie Mac, or Fannie Mae, along with others.  MBSs that are issued by the three government agencies above are guaranteed against default, while MBSs that are issued by other third parties (non-agency mortgages) are not.  This alters the modeling of MBSs.  The simples type of MBS is the pass-through security where a group of mortgages is pooled together, then sold to investors, and investors receive monthly payments representing the interest and principal payments of the underlying mortgages.  The pass-through rate coupon, however, is strictly less than the average coupon rate of the underlying mortgages.  This is due to fees associated with servicing mortgages, as well as profit margins.  

WAC - Weighted Average Coupon Rate is a weighted average of the coupon rates in the mortgage pool with weights equal to mortgage amounts still outstanding

WAM - Weighted Average Maturity  is a weighted average of the remaining months to maturity of each mortgage in the mortgage pool with weights equal to the mortgage amounts outstanding.

They are prepayment conventions that are used by market participants when quoting yields and prices of MBSs. 

CPR - Conditional Prepayment Rate is the annual rate at which a given mortgage pool prepays.  It is expressed as percentage of the current outstanding principal level in the underlying mortgage pool

SMM - Single-Month Mortality Rate is the CPR converted to a monthly rate assuming monthly compounding.

These are related as follows:

In reality, the CPR is stochastic and depends on many economic variables.  However, market participants often use deterministic prepayment schedules as a mechanism to quote MBS yields and option-adjusted spreads.  

The standard benchmark for CPR is the Public Securities Association (PSA) benchmark.

The PSA benchmark assumes:

for 30 year mortgages.  In this case t is the number of months since the mortgage pool originated.  Slower and faster prepayment rates are then given as some percentage or multiple of the PSA benchmark.

Given a particular prepayment schedule, the average life of an MBS is defined as:

where P(k) is the principal (scheduled and projected) paid at time t, TP is the total principal, T is the total number of months, and we divide by 12 so that the average life is measured in years instead of months.  Average life decreases as PSA increases.

In practice, the price of an MBS is observed in the market place and a yield-to-maturity interest rate can be determined.  This rate is the rate that will make the present value of the expected cash flow equal to the market price.  The expected cash flows are determined based on some underlying prepayment assumptions such as 100 PSA, 200 PSA, 300 PSA, etc.  When the yield is quoted as an annual rate based on a semi-annual compounding, it is called a bond-equivalent yield.  These are very limited when evaluating an MBS and fixed income securities in general.  

An investor in a pass-through is exposed to interest rate risk in the fact that any fixed set of cash flows decreases as interest rates increase.  However, a pass-through investor is also exposed to prepayment risk, contraction risk and extension risk. 

When interest rates decline, prepayments tend to increase and the additional prepaid principal can only be invested at lower interest rates.  

When interest rated increase, prepayments tend to decreased and sot there is less prepaid principal that can be invested at higher rates. 

Introduction to Mortgage Mathematics and Mortgage Backed Securities

In this lesson we were introduced to basic mortgage mathematics and mortgage backed securities and the mortgage market.

The mortgage market accounted for 23.3% of the total outstanding amount of US bonds in Q3 2012.  These markets are huge and played a huge role in the financial crisis of 2008 and 2009.
MBSs are a particular class of asset-backed securities.  These are securities backed by underlying pools of securities, such as mortgages, credit card receivable,s auto loans, student loans, etc.  The process by which ABS are created is called "securitization."

Here is an image of how securitization works.  There are 10,000 mortgages and we combine them into one pool.  There are multiple tranches in the pool based on the risk characteristics of the loans.

There are many types of mortgages:

• level-payment mortgages
• adjustable-rate mortgages and
• balloon mortgages

to name a few.  We will only consider level-payment mortgages in these lessons.  A level payment mortgage is a mortgage in which the payment each month is constant over time.

We are going to consider a standard level-payment mortgage with the following assumptions:

• The initial mortgage price M(0) = M
• We assume equal periodic payments of $B
• The coupon rate  is c per period
• There are a total of n repayment periods
• After n payments, the mortgage principal and interest have all been paid (the mortgage is fully amortizing)

This means some of the payment, B, is principal, and some of the payment is interest.

If M(k) denotes the mortgage principal remaining after the k-th period, then

 


where M(n) = 0.
We can iterate this equation from M(0) = (1+c)*M(1)  - B all the way up to M(n-1) = (1+c)*M(n) - B to get the following equation:

but since M(n) = 0, we can plug k=n in this last equation we can say that:

So if we know M, n, and c, we can find the periodic payment amount for the mortg
age.
We can then substitute this B back into the equation above to get:

This tells us the value of the mortgage outstanding as a factor of the initial mortgage amount, the coupon rate, the number of total periods, and the current period.


Now suppose that we want to compute the present value of the mortgage in a deterministic world, with not possibilities of default or prepayments.
Assuming a risk-free interest rate of r per period, we can obtain the fair value of the mortgage as:

Here we are assuming that r is the borrowing interest rate for banks.  In practice, r will not be equal to c.  However,  if r=c, then F(0) = M(0).  In general r < c as banks must charge a higher interest rate so they can account for payment uncertainty, default, prepayment, servicing fees, and profits.

We can also decompose the monthly payment B into the interest component and the principal component.  The interest is:

is the interest that would be due in M(k)
The k-th payment is:

We can use this later to create principal-only and interest-only MBSs.

Pricing Credit Default Swaps

In this lesson, we continued the last lesson of pricing credit default swaps.

The value of the CDS to a buyer is going to be the risk-neutral value of the protection they receive when the bond defaults - the risk-neutral values of the premiums they pay.  We are going to assume that the default event is evenly distributed on the premium interval delta.

Now we will break apart these two factors that make up the value of the CDS.


The risk-neutral value of a single premium payment is: 

Remember that I(t(k)) shows that there is no default and B(t(k)) is the discounting factor (or the cash account or the value of a zcb).  Once again, as in the last lesson, we can break this down into simpler terms.

The risk-neutral value of of all the premium payments is just the sum of the above statement:

The risk-neutral value of the accrued interest if there is a default event between tau = (t(k-1), t(k)] is:

Since the default event is uniformly distributed on delta, the expected value of the uniform distribution of delta is simply (delta/2) which is how we get the above statement.

Therefore combining these values, the risk-neutral value of the premium and the accrued interest is:

We next moved on to the value of the protection.

The risk-neutral value of the protection is:

In this pricing, we assume that R is known, but in reality R is known only on default.  So we are assuming that these CDSs have been around for a while so we know what R will be.

The par spread, or S(par), is that makes the value of the spread that makes the contract equal to zero. S(par) is:

This is simply found by taking the value of the protection minus the value of the premium and accrued interest, setting this equal to zero, and solving for S. 

We then suppose that q(t(k)) = (1-h)*q(t(k) - 1).  We can then approximate the par spread to be:

Credit Default Swaps

In this lesson, we we introduced to credit default swaps.  We were introduced to how credit default swaps give us information about default probability and how these quantities can be used for hedging, investment, and speculation.

The seller of a credit default swap agrees to compensate the buyer in the event of a loan default or some other credit event on a reference entity in return for periodic premium payments.
The buyer pays period payments of d*S*N where:

• N is the notional principle amount of credit protection
• S is the coupon or the spread and
• d is a fraction of a year (d*S is the total coupon that has accumulated over the years)

this keeps on going until some credit event happens (usually a default).  At the next coupon date after this happens, the buyer has to pay the accrued interest d*S.  Also, the seller has to pay (1-R)*N where R is the recovery rate.  

Example:

Consider a 2-year CDS on a notional amount of $1 million with a spread S of 160 basis points (1.6%) and quarterly premium payments. 

Suppose a default occurs in month 16 of the 24 month protection plan and the recovery rate, R, is 45%.

The buyer:

The buyer pays fixed premiums in months 3,6,9,12,15 = (S*N)/4 = $4000

The accrued interest in month 18 (the next coupon date) is (S*N)/12 = $1333.33

The seller:

The default contingent protection payment in month 18 = (1-R)*N = $550,000

The basic model for CDS cash flows is as follows:

Let {t(k) = delta*k = 1,...,t(n)} denote the time of the coupon payments.  For quarterly payments delta = 1/4

If the reference entity is not in default at time t(k), the buyer pays the premium delta*S*N

If the reference entity defaults at time tau contained in (t(k-1), t(k)], then the contract terminates at time t(k).  The buyer pays the accrued interest (t(k) - tau)*S*N and the buyer receives (1-R)*N.  In the last example, the contract terminated at month 18 since default occurred at time tau=16 months between month 15 and month 18.

We then learned about CDS contract details.  CDS contract details were standardized by the International Swaps and Derivatives Association in 1999.  Changes were made in 2003, and 2009, and may happen again if CDS derivates lead to a financial global recession again.  There are so many different details in a contract because there are many difficult issues: how to determine if a credit event occurred, the recovery rate, the spread set for different bonds, when the coupon is paid (advance vs. arrears), and how the spread is quoted.  

The CDS spread S is approximates (1-R)*h where h is the hazard rate, or the conditional probability of default.  For fixed R, CDS spreads are directly proportional to the hazard rate h.  Thus CDS spreads, along with the recovery rate can help determine what the probability of default is for a given defaultable bond.

We then learned about the development and application history of CDS as well as their impact on the financial crisis and the sovereign debt crisis.  I have omitted this portion from this post.