As we discussed last lesson, the following equations correspond to the interest payments of a pass-through security and the principal payments:
remember that c is the coupon rate. This is a level-payment mortgage.
Remember from last lesson that M(k) is:
and we can plug this into the expression for P(k) to give us:
The present value of these principal payments, V(0) is simply the sum of P(k) from k=1 to n over (1+r)^k (this is the discounting factor). We can simplify this to:
This is the present value of the principal payments. We can then use our expression for B from last lesson:
and substitute it into the present value equation to get:

We can also compute the present value of the interest payment revenue stream. The present value, W(0) is simply the sum of I(k) from k=1 to n over (1+r)^k (this is the discounting factor):
This is very simple but it is much easier to recognize that the present value of the interest payments is equal to the total value of the mortgage, F(0), from last lesson, less the principal only payments. F(0) is the fair value of the all the payments in the mortgage and is equal to:
As I said earlier, W(0) = F(0) - V(0), so:
and we can see that when r converges to c, this equal reduces to:
In the next lesson, we will look at the risks for each of these mortgage backed securities.







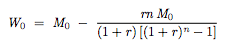
No comments:
Post a Comment