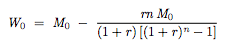Pricing Mortgage-Backed Securities

In this lesson, we learned about prepayment modeling in mortgage backed securities pricing models.  Typically Monte Carlo simulation models are used to price mortgage-backed securities since they are such complex securities.  In this lesson we simply learned a particular prepayment model.

Prepayment models are one of the most important features for pricing MBSs.  However there is relatively little publicly available information concerning prepayment rates, so it is difficult to construct and calibrate the prepayment models.  One model we will focus on is Richard and Rolls's model in which they modeled the conditional prepayment rate (CPR).  Remember that the CPR is the rate at which a given mortgage pool prepays, expressed as a percentage of the current outstanding principal level in the mortgage pool, as an annual rate.  Most prepayment models are private, and used by banks and investment companies and are usually not in the public sphere.

The Richard and Roll model:

 

where:
RI(k) is the refinancing incentive, and is based on the weighted average coupon of the mortgage pool (WAC) and the spot risk-free interest rate.  It represents the amount of money people could save by prepaying and refinancing their mortgage at a lower interest rate.
AGE(k) is the seasoning multiplier, and captures the fact that mortgage owners are very unlikely to prepay in the time periods directly after taking out a mortgage, and are more likely to prepay later in their mortgage rather than sooner.
MM(k) is the monthly multiplier, and reflects that people tend to prepay in different months of the year and each month is fairly close to 1, but do differ slightly depend on the month in question.
BM(k) is the burnout multiplier and it decreases linearly as the mortgage goes on longer.  It simply represents the fact that people who can prepay tend to prepay early rather than later.


We also need to specify a term-structure model in order to fully specify the mortgage pricing model.  The term structure model will be used to:

• discount all of the MBS cash flows into the usual risk-neutral pricing framework and
• to compute the refinancing incentive (the spot free interest rate in RI(k)). 

Whichever term structure model is used it must be able to compute the relevant interest rates analytically.  Such a model would need to be calibrated first.  Then actually pricing the MBS requires Monte-Carlo simulation. 

The sub-prime mortgage market played an important role in the financial crisis in 2008 and 2009.  Sub-prime mortgages were issued to home-owners with very low credit.  Adjustable-rate mortgages were used to lure home-owners in with low interest rates for the first two or three years, then the rates were raised very quickly and the home owners were unable to pay.  Moral hazard problems of mortgage brokers, rating agencies, inadequate regulation, inadequate risk management, and poor corporate governance were other causes that helped lead to the financial crisis as well. 

Collateralized Mortgage Obligations

In this lesson, we were introduced to collateralized mortgage obligations (CMOs).

These are mortgage backed securities that have been created by redirecting cash flows from other mortgage securities.  These are created to mitigate risk. There are many types of CMOs, such as: sequential CMOs, CMOs with accrual  bonds, CMOs with floating-rate and inverse-floating-rate tranches, and planned amortization class (PAC) CMOs.  We will focus on sequential CMOs.

Sequential CMOs have several tranches in a special order such that they are retired sequentially.  For example, a sequential CMO has tranches A, B, C, and D.

1. Periodic coupon interest is disbursed to each tranche on the basis of the amount of principal outstanding in the tranche at the beginning of the period.    
2. All principal payment are disbursed to tranche A until it is paid off entirely.  After tranche A has been paid off, all principal payments are disbursed to tranche B until it is paid off entirely.  And so on and so forth with tranches C and D as well. 

We then went through a excel spreadsheet that detailed how sequential CMOs are created and paid off.
The spreadsheet is in the same MBS download that was included in a previous blog post.

Risks of Principal-Only and Interest-Only MBS

In this lesson, we looked at the risks and exposures of interest-only mortgage backed securities and principal-only mortgage backed securities.

We are going to measure risk by duration.  The duration of a cash flow is a weighted average of the times at which each component of the cash flow is received.  The principal stream has a longer duration than the interest stream of a mortgage since as the age of the mortgage increases, the interest payments will decrease (since they depend on the amount of the mortgage that is yet unpaid) and the principal payments will become a larger part of each monthly payment.  

If we let D(p) denote the duration of the principal stream then:

Where we divide by 12 to convert duration in annual units, rather than monthly units.  We can rewrite this as:

D(p) = the sum from k=1 to n of w(k)*k where 

w(k) = 1/(12*V(0)) * P(k)/(1+r)^k.

In this case is the weight given to each component.

Similarly, we can compute the duration of the interest stream as D(i):

Now we introduce the idea of prepayments.

The interest payment in period k is the same as before:

However, we must reassess the value of M(k) with each prepayment:

where ScheduledPrincipalPayment(k) is now P(k) = B - I(k) for period k.

The risk profiles of interest-only and principal-only MBSs are very different.

Principal-only MBS holders would like prepayments to increase, since they would like their payments earlier (due to the time value of money). 

Interest-only MBS holders would like prepayments to decrease, since the slower the mortgage is paid, the more interest will accrue on the mortgage.  

In an extreme case where all the mortgage holders of a particular MBS prepay their mortgages immediately after taking them out, the interest-only MBS holder will receive zero, since no interest will have been able to accrue on those mortgages.

Principal-Only and Interest-Only MBS

In this module, we discussed principal-only and interest-only mortgage backed securities.

As we discussed last lesson, the following equations correspond to the interest payments of a pass-through security and the principal payments:

remember that c is the coupon rate.  This is a level-payment mortgage.
Remember from last lesson that M(k) is:

and we can plug this into the expression for P(k) to give us:

The present value of these principal payments, V(0) is simply the sum of P(k) from k=1 to n over (1+r)^k (this is the discounting factor).  We can simplify this to:

This is the present value of the principal payments.  We can then use our expression for B from last lesson:

and substitute it into the present value equation to get:






We can also compute the present value of the interest payment revenue stream.  The present value, W(0) is simply the sum of I(k) from k=1 to n over (1+r)^k (this is the discounting factor):

This is very simple but it is much easier to recognize that the present value of the interest payments is equal to the total value of the mortgage, F(0), from last lesson, less the principal only payments.  F(0) is the fair value of the all the payments in the mortgage and is equal to:

As I said earlier, W(0) = F(0) - V(0), so:

and we can see that when r converges to c, this equal reduces to:

In the next lesson, we will look at the risks for each of these mortgage backed securities.